This is post is an overview of the current state of my Tapestry Project

Contents

• Abstract
• Introduction
• Motivation
• Target Developer Experience
• Target Compiler Researcher Experience
• Loom Modular IR
  • Loom Dialects
• Validation Reporting Tooling
• Metakernels
• Graph Rewrite Rules
• Optimization
• Target Environments
• Needs

Abstract

The goal of the Tapestry Project is to provide a complete and developer-friendly aggressive toolchain for generating, visualizing, transforming, compiling, and optimizing AI and scientific computing applications which are optimized for a variety of target architectures.

• Motivation

The existing GPU-accelerated tensor environments (such as PyTorch) are largely focused on providing a near drop-in equivalents for the Numpy Api, and their focus on user-friendliness and compatibility with existing codebases has impeded R&D efforts towards aggressive optimization of tensor applications.

Existing tensor applications often have run costs in the 10k GPU-year range; and even small improvements in the efficiency of the above libraries translates into millions of dollars of savings in power and compute resources.

A ground-up re-imagination of the development tensor algebra is possible on the back of the polyhedral model, and this opens the possibility of a new generation of tensor algebra which is optimized for aggressive re-write operations; replacing small efficiency gains with large double-digit percentage gains.

• Target Developer Experience

The target developer experience should resemble modern SQL or Apache Spark / Apache Beam development, where expressions can be built up using symbolic operations, and passed to either compilers or execution engines which can produce optimized code for a variety of target architectures.

• Target Compiler Researcher Experience

The target compiler researcher experience should permit developers and researches focused in tensor algebras, polyhedral models, compiler optimizations, and system engineering pragmatics (such as RDMA transfers, or GPU kernel programming) to work independently of each other, and to produce and share their work in a way which is compatible with the work of others.

• Loom Modular IR

The Tapestry Project is built upon a modular and extensible IR (intermediate representation) called loom, which permits strict targeted sub-dialects for each transform layer, with appropriate graph semantics constraints, visualizers, and debuggers. This further contributes to layer-isolation for development and research.

By developing and exploiting the layers, symbolic execution graphs can be transformed into concrete polyhedral type operation graphs, and then sharded and optimized for different families of target execution environments.

Directly competing with large existing compiler/language toolchains is an expensive task; and the primary goal of Tapestry is to develop tools at each stage which reduce the future costs of R&D on Tapestry, in support of being able to build the strongest possible optimizer for the restricted polyhedral type tensor block expression algebra which Tapestry represents.

• Needs

We are recruiting project development resources, research and implementation contributors, and grant funding frameworks to further develop the project.

Introduction

The goal of the Tapestry Project is to develop a complete and developer-friendly toolchain for generating, visualizing, transforming, compiling, and optimizing polyhedral type tensor block algebra expressions into optimized code for a variety of target architectures.

That’s a mouthful, so let’s break it down.

A tensor algebra expression is a mathematical expression that involves tensors, which are multidimensional arrays of numbers. For example, a matrix is a 2-dimensional tensor, and a vector is a 1-dimensional tensor. Tensor algebra is a generalization of matrix algebra, and is used in many scientific and engineering applications, such as artificial intelligence, quantum mechanics, fluid dynamics, and computer graphics.

An expression in a tensor algebra derives its value from a series of functional operations performed on one or more tensors; and producing one or more tensors, for example, consider a basic matrix multiplication:

1
2
3
4
5

A := <Tensor of size (m, n)>
B := <Tensor of size (n, p)>

C = MatMul(A, B)
# C := <Tensor of size (m, p)>

In compiler optimization, it is often useful to produce re-write rules, which state that one general form of an expression can be transformed into another form that is at least equivalent, and preferably more efficient to calculate. For example, the above expression can be re-written as a composition of two operations (which in this case will probably not produce any benefit):

1
2
3
4
5
6
7
8

A := <Tensor of size (m, n)>
B := <Tensor of size (n, p)>

Z = Prod(A, B)
# Z := <Tensor of size (m, n, p)>

C = RowSum(Z, axis=1)
# C := <Tensor of size (m, p)>

Lacking further visibility into the internals of the operations, optimizers are limited to re-writing expressions based on these re-write rules; and on altering where and when operations are scheduled to run.

If we observe that many tensor operations are block operations, in that they operate independently on subsets of their inputs in such a way that it is possible to split them into smaller operations and re-combine the results, we begin to see that there is a potential for optimization which looks inside the operations in its restructuring.

The polyhedral model or polytope model provides a framework for describing some block operations in a way which permits direct reasoning about sub-sharding and recombination of the operations; without knowledge of the internals of the operation itself.

The term polyhedral type signature has come to be used to describe the spatial type of an operation as it is described in the polyhedral model. This is a generalization of the term block operation to include the spatial type of the operation.

By extending a tensor block algebra with polyhedral type signatures, we can describe expressions of block operations in a way that permits direct reasoning about sub-sharding and recombination of the component operations, in addition to the above graph re-writing and scheduling.

1
2
3
4
5
6
7
8
9
10
11

A := <Tensor of size (m, n)>
B := <Tensor of size (n, p)>

C0 = MatMul(A, B[1:k])
# C0 := <Tensor of size (m, k)>

C1 = MatMul(A, B[k:])
# C1 := <Tensor of size (m, p - k)>

C = Concatenate([C0, C1], axis=1)
# C := <Tensor of size (m, p)>

This is discussed in much greater detail in the Polyhedral Types and Index Projection document.

A polyhedral type tensor block algebra optimizer toolchain is directly analogous to the SQL model; where the SQL language permits the user to describe the what of a query in terms of relational algebra, and the SQL engine, by applying aggressive query optimization arrives at a query plan which is equivalent to the original query, but is more efficient to execute.

Motivation

The space of GPU-accelerated tensor environments is already dominated by a few well-known ecosystems; most notably PyTorch, TensorFlow, and Jax.

The semantics of these environments take strong motivation from the NumPy API, which is a popular library for numerical computing in Python; and is itself a partial clone of R, a popular language for statistical computing. These statistical libraries have deep roots in the statistical and artificial intelligence communities, and have been optimized for the ease of use of researchers, analysts, and developers working in statistics, signal processing, and artificial intelligence.

As sharding and re-write safe semantics are complex mathematical properties, they are not present by default in expression algebras; the algebras must be carefully designed to support them, and must strictly exclude operations which are not compatible with these properties.

The semantics of NumPy’s operations were not designed with sharding and aggressive re-write operations in mind; and while a large portion of the api surface is compatible with the necessary restrictions, a significant portion is not. Complicating the matter, the libraries are generally embedded in interpreted languages, and frequently intermixed with arbitrary code in those languages.

In order to successfully extract a polyhedral type tensor block algebra expression from a PyTorch program; it is necessary to retro-fit signatures onto PyTorch, to write python code walking analysis, and to force that code to lie inside a complex semantic boundary which is difficult to explain to users. Despite this, due to the high machine costs of large tensor operations, a number of projects attempt to do just this; at larger and larger costs for smaller and smaller gains.

A single training run of a large AI model can cost more than $100M; and the execution lifetime of a trained model can easily consume 10k GPU-years.

A ground-up re-imagination of the development tensor algebra is possible on the back of the polyhedral model, and this opens the possibility of a new generation of tensor algebra which is optimized for aggressive re-write operations; replacing small efficiency gains with large double-digit percentage gains.

The development cost is akin to bootstrapping any new optimizing compiler; and the primary goal of the Tapestry project is to develop tools at each stage which reduce the future costs of R&D on Tapestry, in support of being able to build the strongest possible optimizer for the restricted polyhedral type tensor block expression algebra which Tapestry represents.

The expectation is not a drop-in replacement for PyTorch, Jax, or NumPy; not an environment where Tensor operations freely intermix with arbitrary code; but something more akin to SQL or Apache Spark/Beam, where expressions are built up using symbolic operations, and passed to either compilers or execution engines which can produce optimized code for a variety of target architectures.

If we take the machine budgets of existing AI companies at face value, where some companies have $1B/year machine budgets; finding a 10% improvement in the efficiency of the optimizer would be worth $100M/year to that company.

PyTorch, TensorFlow, and Jax are all pursuing the top-end of this problem; seeking ways to improve the efficiency of code written using their runtime / semantics models, without changing the semantics of the code.

Tapestry is pursuing the bottom-end of this problem; seeking a better foundation for the development of tensor algebra expressions, with a target on never needing to develop program-understanding code scanners, or back port missing semantics to the tensor algebra.

Target Developer Experience

The goal of the Tapestry project is to provide a complete and developer-friendly toolchain for generating, visualizing, transforming, compiling, and optimizing polyhedral type tensor block algebra expressions into optimized code for a variety of target architectures.

The developer experience should resemble modern SQL development; or symbolic execution data flow languages such as Apache Beam or Apache Spark.

Expressions can be built up using symbolic operations (which produce a description of the work, rather than immediately doing the work), and passed to either compilers or execution engines which can produce optimized code for a variety of target architectures.

For example, the following symbolic expression:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

Tensor input = ...;
// dtype: float32
// range:
//   start: [-40, 20]
//   end: [60, 32]
//   shape: (100, 12)

Tensor weights = ...;
// dtype: float32
// range:
//   start: [0, 0]
//   end: [12, 32]
//   shape: [12, 32]

Tensor bias = ...;
// dtype: float32
// range:
//   start: [0]
//   end: [32]
//   shape: [32]

Tnesor z = Linear(input, weights, bias);

Tensor y = Relu(z);

Tapestry.run(y);

Could be expanded and manipulated in various stages of transformation to expand and optimize the code in a variety of ways, and then passed to a compiler or execution engine to produce optimized code for a variety of target architectures:

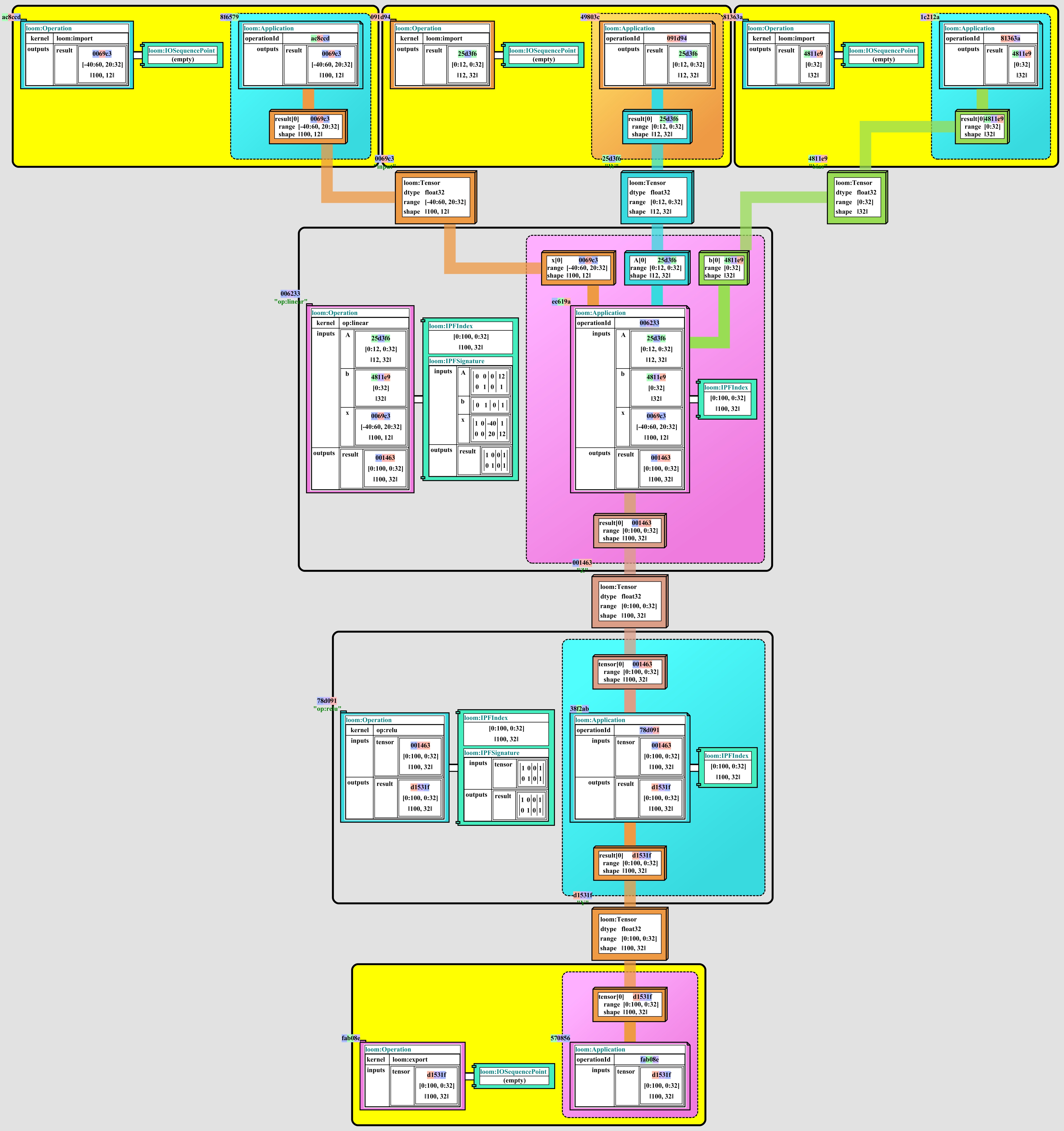
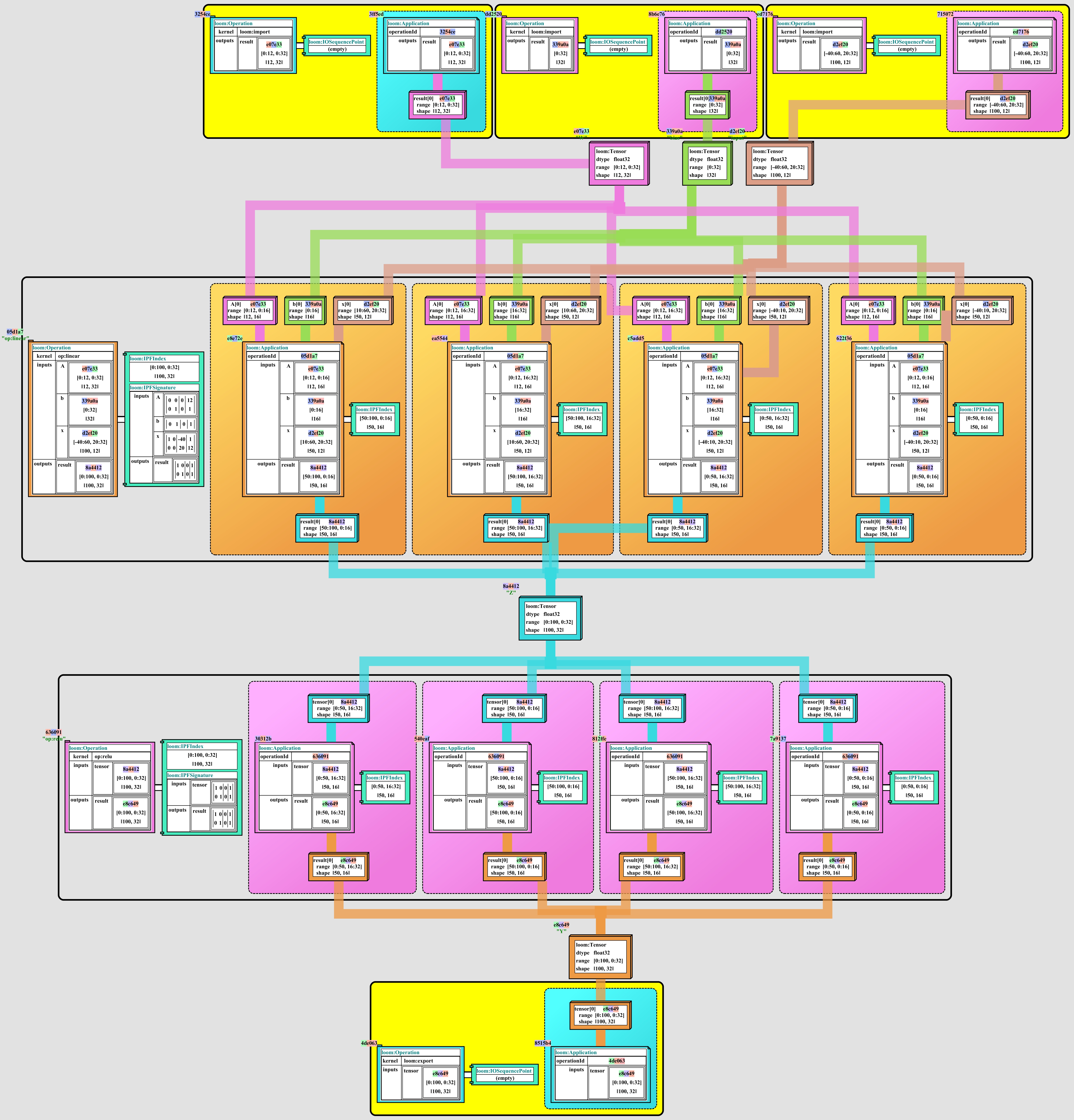
Additionally, the toolchain should provide a rich set of debugging and visualization tools for exploring the intermediate representations of the expressions, and for exploring the optimizations applied to the expressions.

Target Compiler Researcher Experience

• Good R&D Tools => Cheap R&D Cycles
• Cheap R&D Cycles => More R&D Cycles
• More R&D Cycles => Greater Velocity
• Therefore,
  • Good R&D Tools => Greater Velocity

A critical goal of the Tapestry project is to provide as much support to internal development and research teams as possible, to reduce the future costs of R&D on Tapestry.

The development cost of new graph re-write rules, new metakernels, and new target environments and cost models should be easy to write, easy to visualize, easy to validate, and easy to debug.

To this extent, the validation reporting tooling, constraint validation system, and associated tooling for mechanically constructing and reporting complex errors, reporting them in structured data, and visualizing those errors in common formats, such as rendered as text for exception handlers, is a major part of the Tapestry project.

Loom Modular IR

IR is Destiny.

A compiler’s internal representation (commonly called the intermediate representation, as it exists between the source code which was parsed and the target code to be generated) determines most things about the complexity and capabilities of the compiler.

Information which can be retrieved or verified easily in an IR can be used for analysis and manipulation with a little code; information which is fragile or difficult to retrieve or verify requires a lot of code to work with. And code which is difficult to work with is code which is difficult to maintain, and difficult to extend.

In targeting a toolchain which spans from abstract tensor algebra expressions to optimized code for a variety of target architectures, the IR is the most important part of the toolchain; and the ability to extend and constrain the IR for different layers of that toolchain, and for different primitives appropriate to different target architectures, is the most important part of the IR.

Tapestry is designed with a modular IR which permits the easy addition of new node types, node tags, and graph constraints. By selectively including a set of types and constraints, strictly defined sub-dialects can be created which are appropriate for different layers of the toolchain, and for different primitives appropriate to different target architectures.

In this way, toolchain operations which transform from one layer to another can be written in a type-safe way which transform from one dialect to another; and targeted query, debugging, and visualization tools can be written which are appropriate for the layer of the toolchain being targeted.

As the core representation, serialization, and scanning code are shared by all dialects, much of the verification and manipulation code can be shared as well; and the code which is not shared is written in a type-safe way which is appropriate for the layer of the toolchain being targeted.

The Tapestry IR is called loom.

A LoomGraph is a collection of nodes, paired with a LoomEnvironment defining constraints on what constitutes legal values and relationships for those nodes.

A raw LoomGraph is a JSON document collection of nodes:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

{
  "id": "<UUID>",
  "nodes": [
    {
      "id": "<UUID>",
      "label": "<Label>",
      "type": "<Type>",
      "body": <JSON>,
      "tags": {
        "<Type>": <JSON>
      }
    },
    ...
  ]
}

Each LoomNode has:

• id - a unique UUID identifier
• label - an optional, non-unique string label
• type - a string type identifier
• body - a type-dependent JSON structure
• tags - a tag type keyed map of {<type>: <JSON>} of tag type dependent node extensions

Each node type and tag type is expected to have a corresponding schema, defined and enforced by the LoomEnvironment; and is expected to be parsable by type-dependent node wrappers, which understand the data and can provide a type-safe api for manipulating the data.

By defining additional types and constraints, we can compositionally construct language dialects with strict semantics, reusing types and constraints across several dialects.

Example

Assuming two very simple types, a tensor and a simple operation with no sharding information, we could define types and graphs such that a desaturation operation is performed on a tensor of images:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

{
  "id": "d290f1ee-6c54-4b01-90e6-d701748f0851",
  "nodes": [
    {
      "id": "8e3f8f1e-6c54-4b01-90e6-0ae1a048f0851",
      "type": "https://<schema-url>#/types/Tensor",
      "label": "Images",
      "body": {
        "dtype": "uint8",
        "shape": [100, 256, 256, 3]
      }
    },
    {
      "id": "8e3f8f1e-6c54-4b01-90e6-0ae1a048f9000",
      "type": "https://<schema-url>#/types/Tensor",
      "label": "Monochrome",
      "body": {
        "dtype": "uint8",
        "shape": [100, 256, 256]
      }
    },
    {
      "id": "8e3f8f1e-6c54-4b01-90e6-0ae1a048faaaa",
      "type": "https://<schema-url>#/types/Operation",
      "body": {
        "kernel": "desaturate",
        "inputs": ["8e3f8f1e-6c54-4b01-90e6-0ae1a048f0851"],
        "outputs": ["8e3f8f1e-6c54-4b01-90e6-0ae1a048f9000"]
      }
    }
  ]
}

NOTE: The modern XML standards family provides a very strong environment for defining and validating complex data structures. The XML family is also very well-supported in many languages and platforms.

However, the standards which provide the fully fleshed out versions of schemas and query language, the 2.0/3.0 family of XSD, XPath, XQuery, and XSLT, have only one conformant implementation family, which charges very high per-seat licensing fees for the use of the software.

As such, it is not a viable target for an open-source project.

Loom Dialects

The goal of loom dialects are to define strictly limited expression IRs for a targeted layers of the toolchain.

In doing so, we can define:

• An Abstract Expression Dialect for describing applications of tensor algebra expressions, abstracted from the intermediate result shapes.
• An Operation Expression Dialect for describing concrete polyhedral type tensor algebra block expressions, decorated with polyhedral signatures and intermediate result shapes.
• An Application Expression Dialect for describing concrete block sharding of sub-operation applications, and their index locations in the polyhedral index space of their parent operation.
• Families of Target Environment Dialects, expanding the Application Expression Dialect with additional primitives and constraints to represent execution and memory placement and scheduling information for a variety of target environments.

Validation Reporting Tooling

As the a high level goal is to drive the cost of R&D on Tapestry down, a core part of the Loom environment is the constraint validation system, and the associated tooling for mechanically constructing and reporting complex errors, reporting them in structured data, and visualizing those errors in common formats, such as rendered as text for exception handlers.

Consider the following constraint error, detecting reference cycles in a graph:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

@Override
public void validateConstraint(
        @Nonnull @SuppressWarnings("unused") LoomEnvironment env,
        @Nonnull LoomGraph graph,
        @Nonnull ValidationIssueCollector issueCollector
) {
  for (var cycle : TraversalUtils.findOperationSimpleCycles(graph)) {
    var cycleDesc = cycle
          .stream()
          .map(item -> {
            var desc = new HashMap<>();
            desc.put("id", item.getId());
            desc.put("type", item.getType());
            if (item.getLabel() != null) {
              desc.put("label", item.getLabel());
            }
            return desc;
          })
          .toList();

    issueCollector.addIssue(
          ValidationIssue
                  .builder()
                  .type(LoomConstants.Errors.REFERENCE_CYCLE_ERROR)
                  .summary("Reference Cycle detected")
                  .context(b -> b.name("Cycle").data(cycleDesc))
    );
  }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

[
  {
    "type": "ReferenceCycle",
    "summary": "Reference Cycle detected",
    "contexts": [
      {
        "name": "Cycle",
        "data": [
          {
            "id": "3eaa349d-818d-4084-8f71-aaecb2a674cb",
            "label": "Add",
            "type": "http://tensortapestry.org/schemas/loom/2024-01/node_types.jsd#/nodes/Operation"
          },
          {
            "id": "58236994-20f1-4932-add5-3721f609c0aa",
            "label": "A",
            "type": "http://tensortapestry.org/schemas/loom/2024-01/node_types.jsd#/nodes/Tensor"
          }
        ]
      }
    ]
  }
]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

org.tensortapestry.common.validation.LoomValidationError: Validation failed with 1 issues:

* Error [ReferenceCycle]: Reference Cycle detected

  - Cycle::

    |> [ {
    |>   "id" : "d0e577e8-4e3b-450e-a89d-be06db502db6",
    |>   "label" : "Add",
    |>   "type" : "http://tensortapestry.org/schemas/loom/2024-01/node_types.jsd#/nodes/Operation"
    |> }, {
    |>   "id" : "14c9064e-b30a-4d09-84c6-e61d05ba107c",
    |>   "label" : "A",
    |>   "type" : "http://tensortapestry.org/schemas/loom/2024-01/node_types.jsd#/nodes/Tensor"
    |> } ]


	at org.tensortapestry.common.validation.ListValidationIssueCollector.check(ListValidationIssueCollector.java:47)
	at org.tensortapestry.loom.graph.LoomEnvironment.validateGraph(LoomEnvironment.java:175)
	at org.tensortapestry.loom.graph.LoomGraph.validate(LoomGraph.java:164)

Metakernels

The code implementing an operation is generally referred to as the kernel for that operation. Given actual data for an operation, calling the kernel in an appropriate environment will validate the structure of that data (correct parameters and inputs passed, etc), and produce a result.

To describe the behavior of a kernel we do not wish to execute, but to symbolically execute, processing not data, but symbolic descriptions of data, we need a program which will consume the symbolic representation of the inputs and parameters, validate that they are well formed versus the kernel’s expectations, and produce a symbolic representation of the expected outputs of the kernel.

In Tapestry we call this program a metakernel, at it is executed on the symbolic level, rather than the data level.

Tapestry requires that for each kernel we wish to represent in a symbolic execution graph, we have a corresponding metakernel which can be applied to symbolic representations of inputs to describe the kernel’s behavior. Additionally, this metakernel must attach a polyhedral type signature to the symbolic representation of the output, which describes the spatial type of the output in terms of the polyhedral model, to enable re-write and re-sharding operations.

As we need a metakernel for each external kernel in a target execution environment, and as we expect third party libraries and developer applications to frequently provide their own kernels, we need a way to describe metakernels in a way which is easy to write, easy to validate, and easy to share.

Were we required to write a compliant metakernel for each target kernel for each Tapestry compiler environment, the cost of R&D on Tapestry would be very high, and the cost of R&D on Tapestry for third party developers would be even higher.

A major goal of Tapestry is to reduce this cost by developing a portable template environment in which portable template metakernels can be written, validated, and shared.

Consider the following draft-proposal for a template metakernel for a matrix multiplication, which is a common operation in tensor algebra.

In this proposal, we match a shape expression language on the inputs (X and W), such that we extract batch dimensions from the input (X), and constrain $b to match between the X and W inputs. Then polyhedral type signatures are attached to the inputs and outputs in terms of their matched shapes; and a common polyhedral index is used to describe the spatial extent of the operation, and the mapping to the output.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

matmul:
  index: "[$shape..., $a, $c]"

  constraints:
    dtype:
      enum:
        - int32
        - int64
        - float32
        - float64
        - complex64
        - complex128

  inputs:
    X:
      shape: "[$shape..., $a, $b]"
      dtype: "$dtype"

      # this is shorthand for:
      # ipf:
      #   map: "[..., 1, 0]"
      #   shape: "[..., 1, $b]"
      #
      # which is shorthand for:
      # ipf:
      #   map: "[ones($index.size - 2)..., 1, 0]"
      #   shape: "[ones($index.size - 2)..., 1, $b]"
      #
      # Where the map unpacks to a diagonal matrix
      # with 1s on the prefix dimensions.
      ipf: "[..., 1, 0] :> [..., 1, $b]"

    W:
      shape: "[$b, $c]"
      dtype: "$dtype"
      ipf: "[..., 0, 1] :> [..., $b, 1]"

  outputs:
    result:
      # shape defaults to: "[$.index...]"
      # ipf defaults to: "[...] >: [...]"
      dtype: "$dtype"

The work on template metakernels is ongoing, and is expected to be a major part of the Tapestry project.

Graph Rewrite Rules

Graph re-write rules are a common tool in compiler optimization, and are used to describe how one general form of an expression can be transformed into another form that is at least equivalent, and preferably more efficient to calculate. In Tapestry, graph re-write rules are used to describe how one sub-graph expression can be transformed into another equivalent form.

The intention is to heavily leverage the Metakernels template language to describe the behavior of the re-write rules, and to use the same language to describe the behavior of the metakernels which are being re-written.

This work is ongoing, and is expected to be a major part of the Tapestry project.

Optimization

Given a family of semantics preserving re-write and sharding rules, all that is needed in order to produce an initial optimizer is a way to assign value to variations in the graph.

For each given Target Environment, we can develop a target cost model which assigns a vector of labeled costs (wall-clock time, machine count, memory usage, idle resource count) to a graph expression instances.

Plural cost models are perfect fits for Pareto optimization environments; and Pareto optimization environments are embarrassingly parallel, in that we can horizontally add as many additional worker threads or machines as we like, for linear speedups in the optimization search process.

As it is common to encounter AI models which see 10k GPU-year run costs, and as it is common to encounter AI models which are run in production environments with 1000s of machines, the potential impact of even small improvements in the efficiency of the optimizer is quite large.

As the optimizer can be run in parallel, large optimization search spaces can be examined by tasking many search machines, proportional to the expected value of improvements for the given target application.

Over time, research can improve the efficiency of the optimizer, and the quality of the cost models, and the quality of the re-write and sharding rules, and the quality of the metakernels. But even initial versions of the optimizer can be expected to produce significant improvements in the efficiency of the target applications; if sufficient resources are allocated to the optimizer search process.

Target Environments

Each new target environment will likely a new loom dialect, adding primitives and constraints describing placement and scheduling of operations in the target environment.

Each new target environment will likely also require a new symbolic cost model, which assigns a vector of labeled costs (wall-clock time, machine count, memory usage, idle resource count) to a graph expression instance in the target environment’s loom dialect.

There is a possibility of sharing many common kernel (and their associated metakernels) across target environments, and the Tapestry project is expected to develop tooling to support this.

Needs

Tapestry is at a recruiting / growth stage in the project, and we are looking for the following types of support:

R&D Support

We are looking for additional technical and research contributors to help develop the project from initial research stage to a fully functional optimizer targeting PyTorch and Jax backends.

Project Support

We are looking for project management and development resources to help organize the project and recruit additional contributors.

Funding

We are looking for grant funding frameworks to further develop the project.

Historically, languages and compilers have not been successful outside of open source / free software models. Subscription compilers do exist, but as performance options when open reference compilers also exist for an environment. Developers have been historically unwilling to tie their work to a proprietary language or compiler.

Finding a funding model which is compatible with the open source / free software model for the base environment is a major goal of the project.

There are development models where the base environment is open source / free software, and support services are offered to companies which wish to prioritize their extension and development needs for the environment.

There are also models where the base environment is open source / free software, and products are developed which commercially exploit the environment under the same funding structure.

Continuing work on Tapestry, and contrasting with previous explorations of edge-reified graphs as discussed in a previous post; I’ve been exploring a graph IR form with dense nodes, with extension attributes.

When working with extensions, we need namespaces, so I introduced an XMLNS style type, ScopedName, containing:

• a scope (probably a web domain); and
• a name in that scope.

And given this, a handful of basic nodes:

• Tensor Nodes
  • shape attribute
  • dtype attributes
• Operation Nodes
  • signature link
  • input tensor reference map
  • result tensor reference map
• OpSignature Nodes
  • scoped name (with namespace and name)
  • an is-external property

This is sufficient to describe a lowerable graph, but it lacks things needed to describe a schedule (what machine is a thing on), the happens-before links of io nodes (based upon the is-external property), or any information needed to rewrite the graph.

The assumption is that the rewrite rules operate on namespaced properties, and may need new attributes attached to a node to enable novel rewrite rules; so I’m exploring namespaced extension attributes. We can slot the polyhedral type signature into this format, but potentially other information needed for rewrite rules; and it potentially plays nice with xpath/jquery style graph query rules.

At present, this is just a sketch. But it explores ideas of separating core-semantics (tensors, operations, sequencing) from extension semantics (rewrite type information, scheduling constraints).

One thing that’s become clear is that the shape signature of block operations, with their polyhedral projections, is very different from fusion operations like concat; and it’s possible there are yet more special forms needed; rather than force a common form for all operations, or construct an operation hierarchy zoo, it seems profitable to permit namespaced extension attributes, and handle the various forms in purpose-built graph rewrite rules for the given forms.

I’m spending time exploring how to build the type theory for the graphs representing the internals of my Tapestry project.

Consider an expression graph like the following, representing a small expression:

It’s important that this graph lend itself to easy to understand and use APIs, while also being easy to implement fully and correctly. The Tapestry project lives and dies on the ease with which backend compiler and optimizer passes can be written; so the more investment put into getting an expressive yet concise representation I put in, the cheaper and faster everything that follows will be.

Much of that is working out what should be in the graph language; but a lot of that has been done in explorations and theory work on Tapestry so far; under concern at the moment is the internals of the type theory which structures the graph itself.

Node

Consider a simple Node, with an id, making it distinct from other nodes; this will form the basis of most of our type theory:

Note: We’ll use UUIDs for the id; because symbol generation is easy, and because we’d like to be able to compare graphs across a timeline history of mutations to the same graph, so ids in a global namespace work better; we won’t reuse them. Are UUIDs “unique enough”? Almost certainly, yes. We can make sure we don’t reuse them in the same graph, if we really care; but collisions are exceptionally unlikely, and impossible when generated by the same UUID library during the same program execution.

Tensor Node

We know we need Tensors holding values; but our graph model doesn’t see the values, so we mainly need a tensor to represent the space a value could be in. We can extend the Node and add a shape and a dtype:

Structured Edges

We need to establish links between nodes, and some of our links carry data. We can introduce a new kind of node, called an Edge Node, and give it a sourceId and a targetId:

Inputs and Results

We also know that some operations read Tensor Nodes, and some produce them.

We can introduce an Input Edge and a Result Edge, to create that link; but we’ll also include a key field on that edge so we can distinguish which input or output a given tensor is bound to.

We can also introduce some abstract types, HasInputs and HasResults, to describe nodes which are permitted to have these attached edges.

Operation Nodes

We run into problems when we begin to describe operation nodes, representing processes to be applied to tensors to produce new tensors.

We do know that all operations will want to have Parameters, which we can model as part of the node, or as an attached linked node; there are arguments for both, but since we’re aiming to shard operations, we may want to make a choice which permits them to share Parameter nodes after sharding, so we can more easily trace the evolution of sharding plans.

At issue is that we have a number of properties we’d like to be able to attach to an operation node, and the properties don’t fit into a simple type hierarchy.

• Does this operation have external side effects, which we need to sequence appropriately into “Happens Before”/“Happens After” schedules relative to other operations with side effects?
• Is this operation cell-aligned and intrinsically shardable?
• If this operation is not cell-aligned, do we have a block index and shape signature which permit us to shard or slice the operation?

Additionally, we’d like to be able to include operation nodes which are Macro Nodes; which expand into subgraphs of other operations. These can be described by the same properties; side effects, cell-aligned, index and signature bearing.

We can say that “has IO”/“has no IO” is one type property; and “cell-aligned” / “signature” is another, and make the actual presence of the index and signature optional (if it’s missing, we can’t shard).

But a given operation could have either form of either property; determined not by the node type but by the intrinsics of the operation internals being described.

So we’re forced to either:

• expand to the cross-product family of base node types, and special handle each of them;
• annotate each operation with one or the other as a property;
• treat operation classes as CSS-like union properties.

It’s very tempting to try and shoehorn these types into the type theory of existing languages, so that we can take advantage of the language’s static analysis tooling to help us autocomplete compiler backend code during writing, and detect bugs and errors; using either mix-ins or interface extensions; but there is a risk that similar type distinctions will arise in the future, forcing every more elaborate type hacks. And the larger risk is that these type hacks won’t be aligned between languages; the python api may have very different type hierarchies than the java api, for instance.

The alternative to this approach is to build a graph that works more like an HTML/XML DOM tree; where attaching properties and classes to nodes is independent of running schema validators over the tree. The api is somewhat more verbose, and we lose the language’s external static analysis tooling; but we get an api that can be implemented the same way across languages, and we can share schema specifications for type checking.

I’ve put some time into trying to solve this via embedding in Java; and I think I’ve reached the limits of expressibility trying to model the “is IO” relationship; and it’s leading to code that looks like this:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

@JsonTypeName("ResultOf")
@TTagBase.SourceType(TTensor.class)
@TEdgeBase.TargetType(TOperatorBase.class)
@NodeDisplayOptions.NodeAttributes(
    value = {@NodeDisplayOptions.Attribute(name = "fillcolor", value = "#A7E1D5")})
public static final class TResultEdge
    extends TTargetKeyedEdge<TResultEdge, TTensor, TOperatorBase> {
  @JsonCreator
  public TResultEdge(
      @Nullable @JsonProperty(value = "id", required = true) UUID id,
      @Nonnull @JsonProperty(value = "sourceId", required = true) UUID sourceId,
      @Nonnull @JsonProperty(value = "targetId", required = true) UUID targetId,
      @Nonnull @JsonProperty(value = "key", required = true) String key) {
    super(id, sourceId, targetId, key);
  }

  public TResultEdge(@Nonnull UUID sourceId, @Nonnull UUID targetId, @Nonnull String name) {
    this(null, sourceId, targetId, name);
  }

  public TResultEdge(@Nonnull TResultEdge source) {
    this(source.id, source.sourceId, source.targetId, source.key);
  }

  @Override
  public TResultEdge copy() {
    return new TResultEdge(this);
  }
}

So I’m going to explore the DOM tree model next.

This post develops part of this document:

• Tapestry: Shardable Tensor Expression Environments

Tensor View Selections

As noted in previous sections, a family of tensor view selection operations can significantly reduce the complexity of representing expression graphs.

Consider a very simple expression; one which indexes solely over a dimension, mapping vectors of -features to vectors of -features.

The signature for this expression describes the contract of the attached operation; exactly; we do not have analytic information about the internals of the operation (at this level), so to execute this expression, we must provide an input tensor shaped as , and we must expect an output tensor shaped as .

But suppose the previous step provided tensor view , which was oriented feature-first?

What operation might we use to adjust the data?

We could of course use further block expressions to rewrite data; the operation family is general and sufficient for any structural rewrite we may wish to perform. But doing so would push the problem back up a recursion level; we’d be scheduling operations which existed solely to reorder data for other operations.

Under sufficiently strong graph rewrite and operator fusion assumptions, such an approach could work efficiently, but it raises the standards needed for an effective optimizer.

So we look for a weaker operator family, which would be simpler to schedule and more amenable to rewrites and optimization.

Additionally, consider that the input for a given operation may be collected from multiple disparate tensor shards, from distributed execution environments.

Possibly sharded by batch:

Or by feature group:

Defining some terms:

• a Tensor View is a logical slice of tensor-structured data; and
• a Selection is an expression to assemble a Tensor View from other tensors.

Note: a reminder that as these describe sharding operations, Tensor Views are slices of tensor coordinate space; and a given Tensor View may be indexed at any point in tensor space.

A feature which appears to be present from the examined cases is that a Selection routes each cell in its resultant View back to some cell in some source tensor.

We can formalize this as a requirement:

• a Selection maps each coordinate in a Tensor View space to a pair of exactly one source tensor.

Fundamentally, moving data from the output of one operation to the input of another operation, which may be on another machine, is an operation centered on copying portions of buffers; and by being careful in our restriction of legal Selection operations, we can evaluate them by simply copying different buffer data; many of these operations will have zero marginal cost over direct movement.

Affine Selections

Consider the following potential index/stride-manipulation Selection operations:

• permute/transpose - reordering the dimension indexes of a tensor is free.
• reverse/flip - flipping a tensor dimension is free.
• select - selecting a subset of a tensor is free.
• stride - skipping every k items along a dimension is free.
• squeeze/unsqueeze - adding/removing a size-1 dimension is free.
• broadcast^* - treat a size 1 dimension as though it were size n, without copying data.

These operations are free on local tensors, because they’re all indexing tricks; and can be implemented using discrete affine projections, the same as the index projection functions.

On remote tensors, we can transmit the Selection operation to the tensor holder, evaluate the indexing trick operation where it is free, and transmit back the selected data block.

^*broadcast is something we’d much prefer to implement on the local consumer; as implementing broadcast remotely would cause an unnecessary duplication of data. And we see now an operation where a good optimizer may wish to rewrite a Selection cascade for efficiency in some situations.

Composite Selections

A careful reader of the given examples may note that we have a case for both some form of concat (for the example of fusing partial feature results from ); and of interleave (for the example of fusing the results of a sharded dilated convolution kernel).

• concat - assemble a tensor view by concatenating multiple tensors along a dimension.
• interleave - assemble a tensor view by interleaving multiple tensors along a dimension.
• repeat^* - assemble a tensor view by repeating a tensor along a dimension.
• pad^* - supply data outside the selection region with a default value, or a reflection.
• where, max, min - conditionally construct a view by switching on the data from multiple views.

These operations cannot be implemented using discrete affine projections; they generally perform routing by applying some range limit comparison operation, with or without a modulo, to one dimension of the input, and use that to derive a target tensor and new coordinates.

On local machines, concat and interleave are generally implemented as full-copy operations, because otherwise supporting them as transparent views would require a tree of tensor view objects; but as Selection operations, they are still fundamentally performing simple index operations and then differing to a backing view.

^*pad and repeat are Selections we’d also prefer to implement on the local consumer; as the data is either a default value, or a reflection or duplication of data we already have; and these are also good targets for Selection optimization and re-write.

Atomic Selections

We could define a Selection an arbitrary tree of the above or similar operations; but as each of these operations has real impact on the cost model of execution through data sharing impacts, and we desire to be able to see and optimize through those operations; we forbid composite selections:

• All Selection operations are “simple”, and complex Tensor Views are assembled via trees of chained atomic Selections; not composite Selections.

Under evaluation, it will generally be trivial to fuse Selectors; but for analytic modeling, we keep them separate.

An Example From Conv

We now have the operations necessary to fully describe the previous dilated example:

Where a dilated convolution input is sharded into dense convolutions; and the resulting dense results are interleaved back into the convolution result we would have seen if the original convolution had been applied:

Generators

An additional potentially useful category of Selector are generators; consider:

• zeros, ones, full - generate a view full of a given value.
• rand - generate “random” data.

Generators can be used to create an entire Tensor View on the local machine; as the data is a deterministic function, there’s no data to transmit.

Random Generators

It is important to note that rand is an entire sub-category of problems:

• We require an idempotent, and thus deterministic random field; in a given evaluation, we must be able to rebuild the same random values every time a tensor view is accessed; so rand needs a seed and to compute data as some function of the coordinate space.
• There are many random number generation distributions to select from, before we consider that properties (such as ) may be functions of the input coordinates.

It may prove simpler in practice to model random generators as block expressions than as Selector generators.

This post is about notes towards an implementable representation of the “Abstract Expression Graph” / “Sharded Expression Graph” relationship in Tapestry.

Expression languages differ from process languages in that define values in terms of transformations on previous values. The simplest outcome of this is that it’s quite easy to use a given value more than once; but by adding an observer, we can define directly which values are ever observed by the outside world.

Values which are never observed are free to be inlined (when they contribute to other values which transitively are observed), or even eliminated entirely (when they don’t contribute to any observed values).

Simple Expressions

What does it mean for us to be able to observe a tensor value?

• After the expression is evaluated, we can read the value of the tensor.

Chained Expressions

We’re generally interested in more complex expressions, where transformations are applied to tensor values, and then to the results of those transformations, and so on.

In this example, the Tensor: C value is never observed, and so it can dropped entirely from our schedule, or generated and written to a null-store by the block expr.

We are operating with a contract that if we provide the data in A and B to X; that it will correctly produce C and D for us; and that this operation is idempotent.

Additionally, at this level it’s quite possible that the tensors are abstractions which could not fit on a single machine.

Sharded Expressions

We are interested in the ability to:

• shard these operations and values;
• execute a given sharded schedule;
• to compare the costs (in time and space) of different sharding choices;
• and prune expression trees which are not transitivity observed.

This continues the assertion that this is an equivalent and correct sharding; that each of the operations, if performed in dependency order, will produce the same result as the original expression.

Polyhedral Type Information

Being able to say:

• Expression X' is a sharded version of expression X

Is independent of our ability to:

• Verify that X' is a sharded version of X; or
• Given X, generate shareded versions X' and X''

If we have an execution environment for X'; having the sharded version is sufficient for execution.

• Being able to describe the relative components in a tractable manner is the main project.

The additional information, needed to verify and generate sharded versions, is the polyhedral type signature information attached to the expressions.

This is discussed in great detail in Tapestry; the core ideas center around a characteristic shardable index space associated with each expression, and affine projection functions (with resulting fixed marginal steps) from that index space to the spaces of the inputs and outputs.

Finding a concrete representation to describe the relationships between the abstract expression graphs, the polyhedral type information, and the sharded expression graphs is the next major block on this project, in a way which enables us to:

• Verify that the sharded graphs are correct;
• Generate sharded graphs from the abstract graphs;
• Generate abstract graphs from the sharded graphs;
• Apply a cost model to the sharded graphs;
• Write a stochastic optimizer to find good sharding choices.

The cost information

As a consequence of the choice of index spaces and index projection functions for the Tapestry expression representations; we can show that the marginal data sharing costs for input and output have constant marginal costs along each dimension of the index space; e.g. the marginal cost change of including one additional step along a batch dimension is constant, though different, than taking one additional step along a channel dimension.

As the block compute model assumes shardable blocks which are location agnostic in slice space; Assuming that the marginal compute/memory costs of blocks is linearly related to their inputs along the above dimensions; we can take as an abstrac cost model the notion of marginal resource cost per step along each dimension of the index space.

Additionally, at this layer we don’t know what to do with those costs, that is a function of the cost model / scheduling simulator (how are parallel costs managed? are transmission/bandwidth costs elided when a tensor is being moved to the same machine it’s already on; etc.); so we can model costs as fixed marginal costs per step along each dimension of the index space; for each of an arbitrary number of inputs.

Given an index space I with dimensions batch, x, y, k;

We also assume that the transmission of tensors is well modeled, and that the marginal costs associated with the tensors is borne entirely by the marginal data overlap and the transmissions costs.

Additionally, multiple sharded expressions can share the same shape and cost information (as well as information about the operation being modeled).

In this diagram, we’ve added the marginal costs, the index projection functions (Pa(idx)), the abstract and concrete index, and tensor selection slices to the information present in the block expression:

This information is necessary to make any changes to the sharding of the expressions; though it is not necessary to schedule or execute a correct sharding as-is.

Additionally, there’s annotation information we could include or derive, such as:

• the expected size of the input / output tensors
  • when married with a concrete execution schedule, this permits transmission bandwith/delay modeling.
• the expected compute costs of the block
  • CPU/GPU delay
  • Block memory usage

This information about blocks, describing the cost models, is needed in most places where the polyhedral type information is needed.

Encapsulation

When picking graph ownership mechanics, we’re selecting between different encapsulation options to represent the relationship between abstract and sharded expression graphs, and the signatures which describe legal sharding and marginal costs.

Choosing a concrete representation of the above relationships determines the traversal API for the compiler’s cost models, mutation proposers, and debuggers. This in turn affects the development and communication costs of the entire effort.

Previous Work

I speculate that many of the previous efforts in this space have struggled under the requirement that they start with a concrete expression sharding, and work backwards attempting to derive an abstract graph and operator signatures for the associated expressions, and then to produce transformations which maintain the semantics of the original expressions.

And this has been difficult, because many of the languages in question lack particularly strong shape signature information; most of the development effort seems to get soaked up in this code analysis phase.

“ZSpace” is a common shorthand, typographically simple name for the infinite family of -dimensional discrete Euclidean spaces.

The -dimensional coordinates of discrete-celled tensors (the kind of tensors we work with on computers) are ZSpace objects, as are bounding regions selecting those coordinates, and morphisms or maps from one region to another.

Though we could, in principle, simply call a coordinate an array of integers; performing any non-trivial index math on discrete location -dimensional tensors requires libraries for representing and manipulating these tensors.

As I’ve been working on pieces of Tapestry: Shardable Tensor Expression Environments; most of the work has be focused on libraries for manipulating objects in ZSpace without spending all of my time debugging math errors.

Most tensor libraries I’ve been able to examine, for Python, C++, Java, and Rust, focus primarily on abstracting the details of using hardware accelerated vectorized floating point operations. They carry big dependency costs, and have lots of runtime call patterns, driven by this.

So I’ve been building my own ZSpace libs, which cannot represent anything other than integer values; because my focus isn’t on the performance of the calculations of the data in the values; but on correctly manipulating (with type checking and runtime assertions) index regions describing shards of expressions.

This is, for instance, the ZTensor and tests:

• ZTensor.java
• ZTensorTest.java

This is a situation where the existing libraries were just not built for manipulating polyhedral types and ranges in ZSpace; where we frequently wish to perform transforms which result in coordinates.

There’s a tremendous amount of clever little tricks wrapped up in how tensor libs get built; and how things like transpopse, permute, reverse, select, squeeze, unsqueeze, and broadcastTo can be implemented with zero-copy views which read or write back to their parent; and I may do a series on “How to write a Tensor”; but for now a fair number of those tricks are wrapped up in that code.

Side Note: Size, Z^0, and Scalars

The size of a contiguous slice of ZSpace (the number of elements contained in it), and thus of a contiguous slice of a tensor; is the product of the size of the inclusive bounds of that slice; aka, the shape of the tensor.

• In , simple arrays, the size is trivially the length of the array;
• In , simple matrices, the size is , the product of the dimensions;
• and so on for

However, consider the -dimensional space . The product of an empty collection is defined as ; as this is the most consistent answer for a “zero” for multiplication; so we have this argument for the existence of -dimensional tensors which still have one element in them; purely from the math of the product of shapes.

And it turns out, that’s how all tensor libraries model scalar values; as -dimensional tensors.

This post develops part of this document:

• Tapestry: Shardable Tensor Expression Environments

Sharding Convolution Operators

Let’s now consider a new operation, the application of Convolution Kernels.

1

Y = Conv2D(X, K)

Kernel convolution operations tile (or tessellate) a moving input window over the entire space of an input tensor. Convolution operations (frequently, see sparse convolutions below) share input data with neighbors; and effective modeling of their shard characteristics can dramatically reduce data flow in large computations, by sharding data neighborhoods to maximize local data sharing.

Expanding the sharding theory of convolution operations will require us to:

• define tensor stride view operations, to model sparse convolutions;
• develop stacked affine projections, to work in derived view environments;
• define tensor fusion operations, to reassemble sparse shards.

Consider the following case of a kernel. We wish to generate output cells by applying an operation on this kernel to window selections on the input of the same size.

If we apply no padding, and shift each neighbor by 1 step:

• ;
• ;
• ;
• etc …

The projection function for the no-padding, simple stride, dense case is very simple to describe:

• the origin value should point to the first cell used by the output origin;
• the marginal stride matches the output stride;
• the projection shape size matches the window size.

In this situation:

• is ,
• is

Convolution operations are frequently applied to not one convolution kernel, but to a stack of them. It’s common for a call to have a kernel (or filter) with a 2D or shape, but with , stacked filters; so we may see , and to produce a layer of for each input filter layer.

Additionally, in cases where no padding is used, the output must lose size relative to the input; the first and last values along each dimension are shifted in to permit the full selection of the convolution filters. Padding will be discussed later, which brings with it many questions of how that padding should be generated.

Consider:

• a 100 batch, shape, 1-channel input ;
• a 128 layer, shape, 1-channel input convolution filter ;
• yielding a 100 batch, shape, 128-channel output .

Sparse Strided Convolution Operators

Consider an operation which is common in convolution, but which our current index projection description has no mechanism for describing: striding

In this example, we wish to apply the kernel filters to tiles of the input; but we wish to do that sparsely along one of the dimensions; skipping over 1 value in our selection.

This is a common mechanism to add non-local information to a kernel without inflating the size (and complexity) of the kernel filter itself; a good model of it is necessary.

The outcome we’d like to achieve in this situation is that we’re able to rewrite this operation into dense variants; doing so permits local neighborhood data reuse.

Consider the following rewrite, into strided sliced views of ; and fusing from strided sliced result shards:

There are two broad approaches to realize this goal, which will be explored in later sections:

• extending the projection function language with the concept of striding;
• developing strided tensor slice and fusion operations.

In practice, these two approaches are isomorphic to each other; though in some situations some problems are easier to express in one or the other approach. We’ll develop both.

This post develops part of this document:

• Tapestry: Shardable Tensor Expression Environments

Graph Rewrite Rules

Graph rewriting is a common implementation feature of graph evaluation languages; “graph rewrite rules” are rules to describe legal rewrites on a graph, and the field constitutes a large field of study on its own.

As an example, suppose we have a graph containing the following subgraph:

And we have a rule saying something like:

• “Under certain conditions, A can be rewritten in terms of J and K”; with appropriate patterns and machinery to check those conditions, and perform the rewrite mechanically.

We could imagine determining that the rewrite applied in this situation, and then applying it yielding the following graph, where A has been replaced with J and K, and an intermediate value V has been introduced:

It can be valuable to distinguish between semantic and optimization rewrites:

• semantic rewrites are rewrites required by the language; frequently when some high level feature is implemented in terms of lower level features, and must be replaced for evaluation.
• optimization rewrites are rewrites which aim to reduce the execution cost; they are optional, but desired.

Much of the work on block sharding thus far has been implicitly modeling families of rewrite rules around sharding block operations; on rewriting block operation graphs, such as this one:

Into graphs where the block operations have been sharded in some way, such as this one:

Previous work in sharding and blocks has shown that there are other rewrites that are valuable to us, starting from a high-level block:

We semantically rewrite to either a if we choose not to shard on the dimension of :

Or we semantically rewrite to a , , subgraph if we choose to shard on the dimension of :

Fully expanding an optimizing tensor evaluation environment requires some facility for graph rewriting; though only semantic rewrites are required.

Optimization rewrites are frequently treated as a nice-to-have; something added to evaluation systems once they’ve reached maturity, and added piecemeal, where they can be inserted without disrupting the semantics of existing programs.

The resource impact, in performance and memory, of optimization rewrites can be extremely large; large enough that an argument can be made that the core structure of a system should be engineered from the beginning to enable them; and that is the approach that we’re taking with Tapestry.

Graph rewrite rules, both semantic and optimization, require a mechanism of application. There are two broad categories of graph rewrite application methodologies:

• Local Expansion - locally expanding a node with the subgraph which “defines” it.
• Global Search - searching for subgraph patterns in the full graph which match a given rule, and rewriting the matching subgraph.

Local Node Expansion Rewrite

Local node expansion is the simplest form of graph rewrite to implement.

Local node expansion rules are best thought of as production rules:

• they mave have a single expansion,
• they may have multiple ambiguous expansions,
• they may have conditional expansions which can only be used in certain situations;
• and they may be recursively defined with other production rules.

Given a high level node, such as this example , local rewrite provides one or more expansions for the definition of that node. We need only find that node in the tree, and replace it with one of it’s “definitions”.

For example, consider this subgraph featuring :

A high level node with a single expansion is essentially a simple function or macro. In this case it’s easy and common to think of the expansion as the “definition” or “internals” of the .

Suppose we had one expansion defined for ; such that the following rewrite could be applied:

A given high-level node may have multiple expansions; which is equivalent to plural production rules; for example this entirely different rewrite of .

Conditional Rewrites

In the situation where there are multiple expansions of a given node, it is common to set some conditional gates upon those expansions; to establish a guarantee that a given node will be expanded unambiguously in exactly one way in a given situation; frequently with fall-through precedence ordering, and a final default case, to handle resolution when multiple tests match:

• If condition is true, expand to ;
• If condition is true, expand to ;
• otherwise, expand to .

This is helpful with single descent local rewrite implementations; but it is limiting for global optimization.

Ambiguous Rewrites

If we permit multiple expansions of a node to simultaneously match, either by having no conditions on expansion, or by permitting more than one condition to match at the same time, we may have ambiguous expansion.

A simple fall-back implementation to handle ambiguous expansion is to apply some heuristic to select the winning expansion; but the real power in ambiguous expansions lies in global optimization.

It is frequently the case that there isn’t sufficient local information to determine which expansion is best; and we can only determine the best choice by examining the relative cost models of both expansions in a global context.

Implementing parallel global tree optimization search is significantly more complex and expensive at compile time; but also permits much more aggressive optimizations; particularly when paired with global pattern search rewrites, as discussed below.

Global Pattern Search Rewrite

Global pattern search rewrites are not limited to defining local expansions of high-level abstract nodes.

Global pattern search rewrites define subgraph patterns that they can be applied to (potentially gated by conditional tests); and upon application they can rewrite the tree at that location.

Consider the subgraph below:

Suppose we had a rule which could match the pattern, and rewrite it to a new condensed operator, :

This rule is not a node expansion; and to apply a rule like this, we’d need to search the entire graph for matching patterns.

Suites of global graph rewrite rules can enable deep incremental rewrites, particularly when their rewrites are permitted to be mutually recursive (produce rewrites which will in turn be rewritten).

Implementations of the application of global rewrite rules can be grouped into two broad categories:

• deterministic/fixed-pass count implementations - these scan for patterns a fixed number of times, performing expansions and rewrites in a predetermined order.
• non-deterministic implementations - these scan for matching patterns until a fixed-point is reached; a point at which no further rewrites can be found.

It is common to stack rewrite passes into larger rewrite meta sequences; deterministic passes to expand certain high level primitives; a few non-deterministic passes to search for optimizations; and a few final deterministic passes to perform fusions.

As discussed later in the sections on parallel stochastic search; we can see that each re-write step will produce an instance with a different estimated cost according to our cost models, and we can merge rewrites with stochastic optimization to allow us to use the ambiguity of optional rewrites to permit aggressive exploration of the optimization space.

Returning to Linear

Returning to the implementation of expansion; we could implement using either local expansion, or global rewrite search.

Linear under Local Expansion

Under local expansion, we’d implement with expansion rules on the operator, expanding to either a if we choose not to shard on the dimension of :

Or expanding to a , , subgraph if we choose to shard on the dimension of :

Linear under Global Rewrite

Under global rewrite rules, we’d always expand to the , , representation:

But we’d also add a global rule that said that the pattern could be conditionally rewritten to when the dimension wasn’t being sharded upon:

One of the benefits of this approach is that any matching subgraph with these operators could be fused anywhere in the graph, even if they’d never originally been part of a block.

Graph Fusion Operators

Global rewrite operations become significantly more powerful when paired with fusion operators designed for them.

We can examine common operators, and develop a repertoire of utility operators, sometimes with interfaces which may seem less natural for programmers to use directly, which significantly improve fusion products.

This is a common approach in functional language compilers, such as Haskell.

This approach can be made more powerful when high-level operators are designed by api designers in terms of the known family of fusion operators and rewrite operations; leading to potentially large wins in fusion optimization search results.

Next

The next focus will be on developing the mechanics to show that the sharding of convolution operators can be cleanly expressed in index projection functions and graph rewrite rules; and beginning to discuss implicit tensor view, shard, and fusion operators.

This post develops part of this document:

• Tapestry: Shardable Tensor Expression Languages

Parallel Stochastic Optimization

The tapestry work thus far has focused on establishing rewrite rules to find equivalent evaluation graphs to an initial high-level abstract program. Given an initial graph in a system of formal semantics, we have established rules which permit us to mechanically derive a large family of alternative graphs (, , , …) which evaluate to the same results under that system of formal semantics.

Tapestry is designed to be amenable to parallel stochastic multi-objective optimization; the choices made thus far have focused on enabling effective use of parallel optimizer search.

An optimizer can be described, at a very high level, as a process to take an initial graph , a cost model , and a family of rewrite rules , and select the lowest-cost graph it can find.

In some optimization problems, the cost model returns not a single value, but a collection of values we might be simultaneously interested in improving. For example:

• the total memory usage
• the total compute usage
• the expected wall-clock time
• the peak node memory usage
• the peak node compute usage
• the node memory utilization waste
• the node compute utilization waste

Stochastic Pareto Frontier Optimization

Enter the field of multi-objective optimization; which is the research field into optimization when we have multiple dimensions to care about. This section is a brief overview of multi-objective optimization, as it applies to tapestry plans.

Given an existing population of instance trials , we can run our cost model on each trial , and produce a multi-dimensional cost value. Placing those costs in space, we can establish a surface known as the “Pareto frontier”, made up of all instances which are better than any other instance on at least one dimension:

The Pareto frontier represents the instances (found so far) making the best trade-offs between resources we care about from our cost model.

When searching for improvements, we can select one (or more, in the case of graph or genetic cross-over) instance(s) of the instances from the pareto frontier (or, in the case of some models, sampled proportionally relative to their distance from the frontier); apply one or more of the mutation rules, producing a new instance , and run the cost model to establish the new cost , placing the new instance somewhere in the optimization space:

With the addition of a new cost-annotated instance, we recompute the pareto frontier; if the new instance represents an improvement, we move the frontier:

There are many ways to improve this. It’s common to sample parent instances from points near the frontier, even if they no longer lie upon it; and the generalization of that is to say that there’s distribution of parent selection probability which is willing to sample any instance within some distance of the frontier with some probability relative to that distance.

A large motivation for the sampling approach is that many mutations may not produce better children, but might enable further mutations which do, and we don’t want to close ourselves to exploring those options.

Further, it may be the case that there are regions of the optimization space which constitute external constraints; but we’d still like to include instances outside that region to permit appropriate exploration.

For example, our initial graph likely has peak node memory and compute utilization greater than any of our existing compute resources; we can’t schedule it at all, but it’s the basis for our initial optimization search.

Graph Mutator Selection Optimization

There’s also a host of research about how to balance selecting which mutation rules from our collection of mutation rules to apply.

In practice, not every mutator rule can apply to every graph; so we can extend our description of mutations to include applicability rules ; such that for a given instance, we only consider rules where the applicability test for the rule says it applies.

We could select from these rules uniformly, or hand-code their firing probabilities. In practice, it is common to tune the triggering rate for optimization rules against metrics collected over a series of benchmarks.

As long as every rule has a chance to apply, and every instance has a chance to be selected, then the entire space of legal graphs constructed by some series of mutations is reachable; though it may be intractable to fully search, so we’d like to bias our exploration to things likely to yield improvements.

One approach is to track the mutation histories of each instance (the series of mutation rules which lead to each instance), and compute the rates at which each mutation rule contributed to improvements in the pareto frontier.

This can be done offline, by running benchmarks and hard-coding the resulting values; or it can be done dynamically while running a given optimization.

In practice, a combination approach is powerful: offline benchmarking to establish a prior distribution, combined with dynamic statistics based in the observed optimization histories attached to a given problem.

One additional value of dynamic mutator rule balancing is that it eases use of third-party and application-specific mutations rules.

Parallel Optimization

Given that our instances are very small relative to the data they operate on (they describe execution graphs), and our cost models are relatively abstract (they compute expected compute and memory and timing costs for a given graph); we expect that examining any given instance will be very fast and small, compared to actually running the described execution.

If optimization evaluation is sufficiently fast and small, and if mutators have a high enough chance of producing improvements, a local optimization loop running on one machine, in one thread, has a good chance of producing a good execution graph for our needs.

But if the graph is complicated, or the rules do not immediately produce improvements, or if the graph optimization surface has lots of local minima; we may need to examine parallel optimization.

Parallel optimization is running trials in multiple threads, or even potentially on multiple machines, in parallel. Stochastic pareto front optimization is well suited for parallel optimization; at the limit, machines only need to communicate when they’ve found improvements to the pareto frontier. Optimizing this form of search is a large field of research.

One interesting approach to take is to run the search as long as continuing to do so is expected to reduce the total value of some function of the cost model.

Say, we’re currently seeing a 5% improvement every 1000 trials of the optimization search? When should we stop looking for a better answer? An optimal choice depends on:

• how expensive are the optimization trials?
• how valuable is that 5% reduction in the optimized graph schedule?

When targeting jobs meant to run for weeks to months on 1000s of GPUs; we may reasonably aim to run the optimizer on 100 machines for a few hours, if doing so reliably reduces the long term utilization.

However, when targeting jobs which should take 5 machines 20 minutes; the target optimization time should probably be a great deal shorter.

This post develops part of this document:

• Tapestry: Shardable Tensor Expression Environments

The Tapestry Vision

To explain the larger vision of Tapestry, we need to explore the uses cases of a large system which does not yet exist, which we’ll also call A Tapestry.

Note: The motivation for the synecdoche here is taken from SQL, where SQL is both the language and the environment, as their semantics are formal and shared.

Grid-scale datacenters filled with GPU nodes are becoming commonplace; datacenters with 1000s of server-grade GPUs, commonly hosted on densely networked machines with 2-8 GPUs per machine. These machines have tremendous theoretical compute throughput, but existing programming environments for them require multiple layers of systems engineers and operations engineers to successfully exploit the theoretical potential.

Common use involves compiling specialized application images for a given task to be run on these systems, allocating some subset of the available machines as machines for that task, pushing machine images to each machine allocated for that subset, and running a controller and worker instances built from the compiled application image. The entire workflow is inefficient and fragile, and encourages sizing datacenter usage to the max storage or compute needs that a task will need for its entire lifecycle.

Suppose we instead had a uniform collection of interconnected nodes with unified management, holding both storage and compute resources. Interconnected service grids where point-to-point communication is abstracted into semantic routing are frequently called “meshes” and “fabrics”; to be specific here we’ll call this:

• a tensor fabric, or
• a tapestry environment

The individual nodes in this environment would be largely opaque to us; we would not send data or jobs to them individually, or push virtual machine images to them; they act in concert as a unified environment, and we work with them in terms of the total environment.

One way of thinking of this is as a very large numpy or torch environment.

Suppose we can perform a few operations in this environment:

• Allocate and manage named tensors in the environment.
• Copy portions of tensors into other tensors.
• Load and export external data into and from named tensors in the environment; for example from and to databases and network file sources.

This is a very basic environment; and for now, we’ve omitted a number of details.

• How is the data split between nodes?
• How is node recovery managed (do we have duplicate copies of the data)?

Given only the ability to create storage, move data around, and move data into and out of the tapestry; we’ve defined an environment with scratch-space semantics. We could find a use for this environment; run data jobs which unpack their data and construct large tensor objects, followed by data jobs which re-pack that data differently.

Now, suppose in addition to injecting data into our environment, we’d like to be able to inject functions which manipulate the data. The environment has many compute nodes, but they’re distributed; it stores a lot of data, but not in places or shards we know about.

To be able to inject functions, we desire a way to describe semantic actions we wish to take on the data (“apply this function to that tensor, yielding a new tensor”):

• without specifying the details of the layout or scheduling,
• while getting close to theoretically resource optimal results.

A high-level desired workflow would permit us to:

1. Load tensor data into tapestry:
2. Inject and apply an operation, transforming existing tensors into new tensors:
3. Export the result tensor data:

The details of the operation injection step are the crucial issue here; finding a family of operations which can be injected into such an environment and yield optimal resource (time and space) efficient results with minimal external knowledge about the tapestry layout.

Many environments exist for flat-mapped collections, for data that is structured in lists, arrays, or key/value mapped dictionaries:

• Apache Spark
• Google Dataflow

These environments do not model tensor-indexed values, or have effective mechanisms for distributing dataflow and functional dependencies across polyhedrally typed operations; a new formalism is needed to effectively describe operator injection into distributed tensor environments.

Tapestry is an effort to describe such a formalism, focusing on shardable by construction operation graph semantics.

Applications

A brief review of some applications of a tapestry environment.

Artificial Intelligence / Machine Learning

Deep learning AI/ML applications describe models as stacks of tensor-valued weights, connected by a computation graph describing how tensor-valued data injected into the model evolves through a series of compute steps to produce the predictions of the model, or to compute changes to the models weights for learning.

Existing systems are built on stacks of numpy-inspired APIs, with minimal optimization passes; an API which was not designed to restrict itself to shardable operations. As a result, existing systems struggle with operational engineering to achieve effective distribution and sharding, and leave a great deal of theoretical throughput unexploited.

An optimizing tapestry environment could greatly speed AI/ML research, by removing the requirements for much of the task-specific operational scaling engineering; while simultaneously reducing the research costs, by optimizing the resulting operations graphs to more effectively utilize available resources.

Finite Element Simulations

Finite element simulations decompose a problem (weather, heat flow, stress) onto tensors describing a space to be simulated, valued in terms of the material properties at each point in the space (density, energy, pressure, material, heat, etc).

Finite element simulations evolve by describing a kernel transition function, which predicts the next time value for a given point in space by applying a kernel transition function which examines only the tensor values of the local neighborhood of that point at the previous time value.

This is equivalent to iteratively applying a kernel convolution to produce successive time step world tensors.

An effective tapestry environment sufficient to host finite element simulations would permit accelerated research into anything built upon finite element simulations; which includes a great deal of modern engineering and physical sciences applications.